Mathwords Maclaurin Series

The Basic Maclaurin Series. Math 1220 (Spring 2003) Here are the basic Maclaurin Series from which you can build most any. Maclaurin series you'd ever need by doing algebra or calculus. 1. The Maclaurin series of the exponential has convergence set (1. ;
Maclaurin series ln(1+x) YouTube

If x = 0, then this series is known as the Maclaurin series for f. Definition 5.4.1: Maclaurin and Taylor series. If f has derivatives of all orders at x = a, then the Taylor series for the function f at a is. ∞ ∑ n = 0f ( n) (a) n! (x − a)n = f(a) + f′ (a)(x − a) + f ″ (a) 2! (x − a)2 + ⋯ + f ( n) (a) n! (x − a)n + ⋯.
SOLVEDUse a Maclaurin expansion to find each integral. ∫ln(1+x) d x

The five steps for determining the Maclaurin Series of f(x) = ln(1+x) are as follows. Find derivatives for f(x) Evaluate these derivatives and f(x) at x = 0 ; Assemble the sum of products ;
PPT Lesson 7 Maclaurin Series PowerPoint Presentation, free download ID5397657
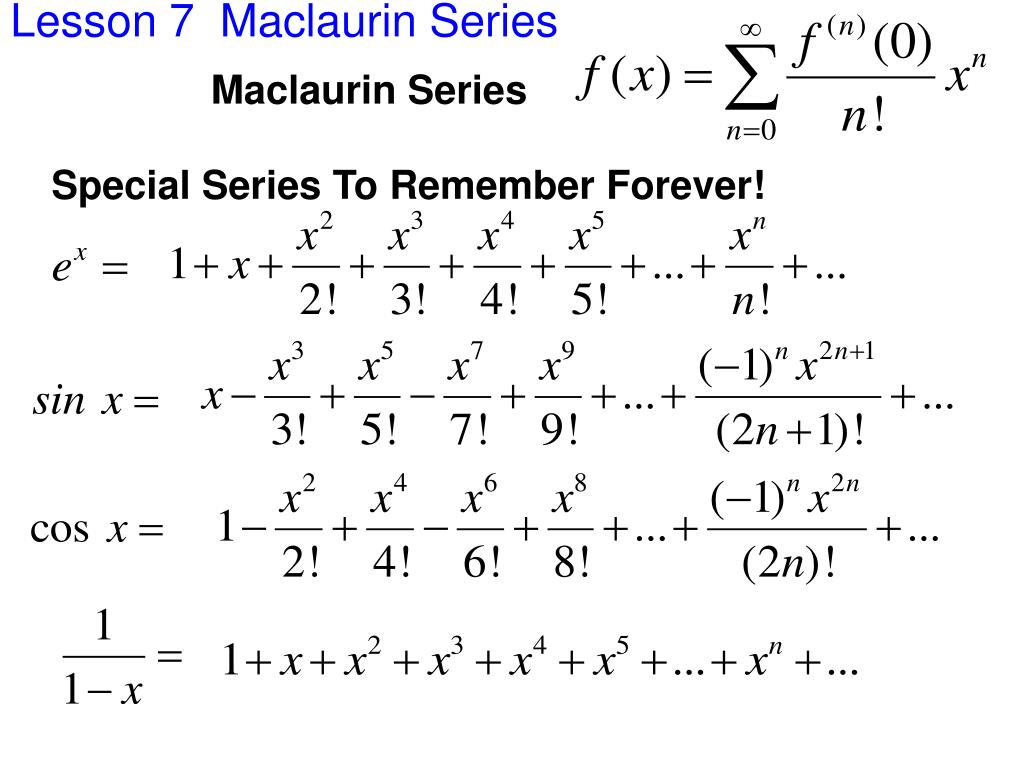
Aug 29, 2014. The Maclaurin series of f (x) = ln(1 + x) is: f (x) = ∞ ∑ n=0( −1)n xn+1 n +1, where |x| < 1. First, let us find the Maclaurin series for. f '(x) = 1 1 +x = 1 1 −( − x). Remember that. 1 1 − x = ∞ ∑ n=0xn if |x| < 1. (Note: This can be justified by viewing it as a geometric series.)
How to find the Maclaurin Series of 1/x YouTube

maclaurin series calculator. Have a question about using Wolfram|Alpha? Contact Pro Premium Expert Support ». Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music….
Use Maclaurin series table to obtain series for f(x) = x^2 ln(1+ x^3). Find radius of

The Maclaurin series is named after the Scottish mathematician Colin Maclaurin (1698-1746), who independently discovered this concept. Maclaurin explained how to use the series to approximate functions near 0 and solve problems in various fields.
Solved Using the Maclaurin series for ln(1 + x), find the

Maclaurin Series of ln (1+x) In this tutorial we shall derive the series expansion of the trigonometric function ln(1 + x) ln. . ( 1 + x) by using Maclaurin's series expansion function. Consider the function of the form. f(x) = ln(1 + x) f ( x) = ln. . ( 1 + x) Using x = 0 x = 0, the given equation function becomes.
Maclaurin series ln(1+x) YouTube

Find the Maclaurin series expansion of a function. Get the free "Maclaurin Series" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.
Ex Find a Maclaurin Polynomial and the Interval for a Given Error ln(1+x) YouTube

maclaurin series ln (1+x) Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music….
Maclaurin Series for ln(1+x) Howto & Steps Video & Lesson Transcript

Maclaurin series ln (1+x) | Desmos. Loading. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.
Maclaurin Series of ln(1+x) YouTube

Maclaurin series of sin(x), cos(x), and eˣ. In the real world you'd start with ln(1+x^3) and try to find its expanded form (approximation) by taking the derivative, expanding, and then integrating -- you wouldn't start with a geometric series and integrate its closed form because you're just looking for something "neat" to do.
Maclaurin Series Formula Learn the Formula of Maclaurin Series

Overview of Taylor/Maclaurin Series. Consider a function f f that has a power series representation at x = a. x = a. Then the series has the form.. Figure 6.5 The function y = ln x y = ln x and the Taylor polynomials p 0, p 1, p 2 p 0, p 1, p 2 and p 3 p 3 at x = 1 x = 1 are plotted on this graph. Checkpoint 6.10.
SOLVEDFind the Maclaurin series for the following functions. \cos [\ln (1+x)]
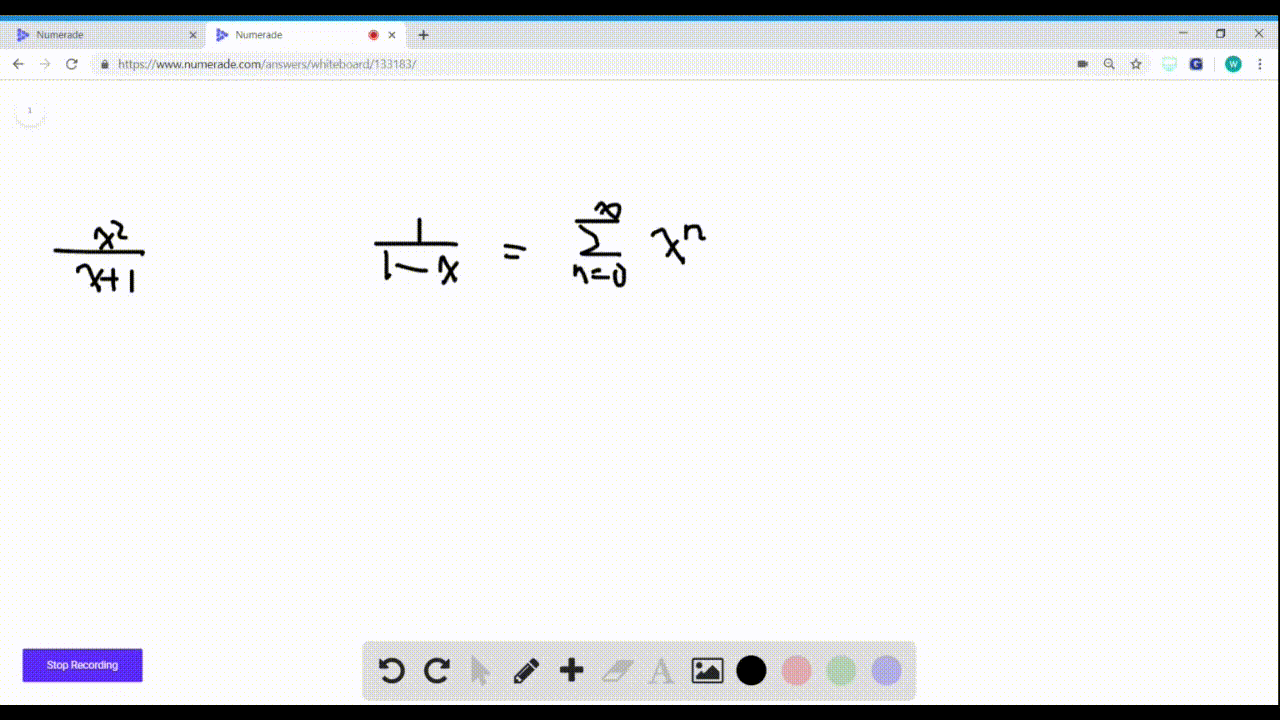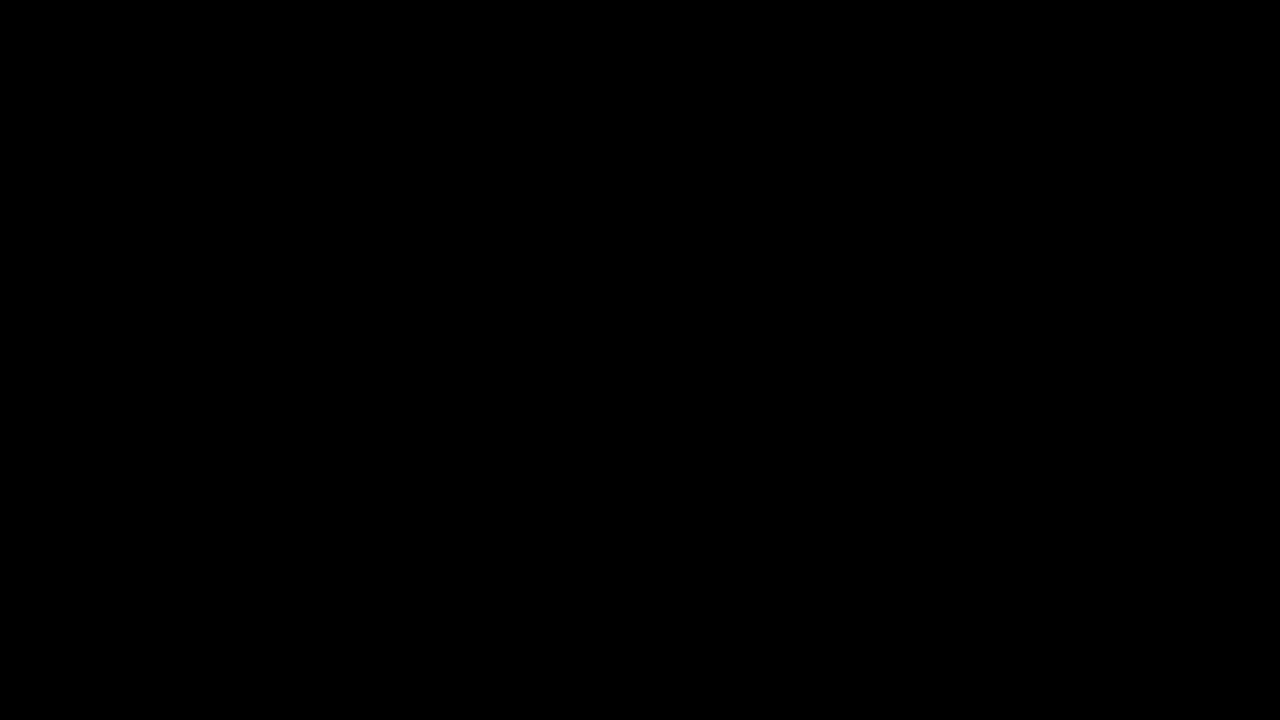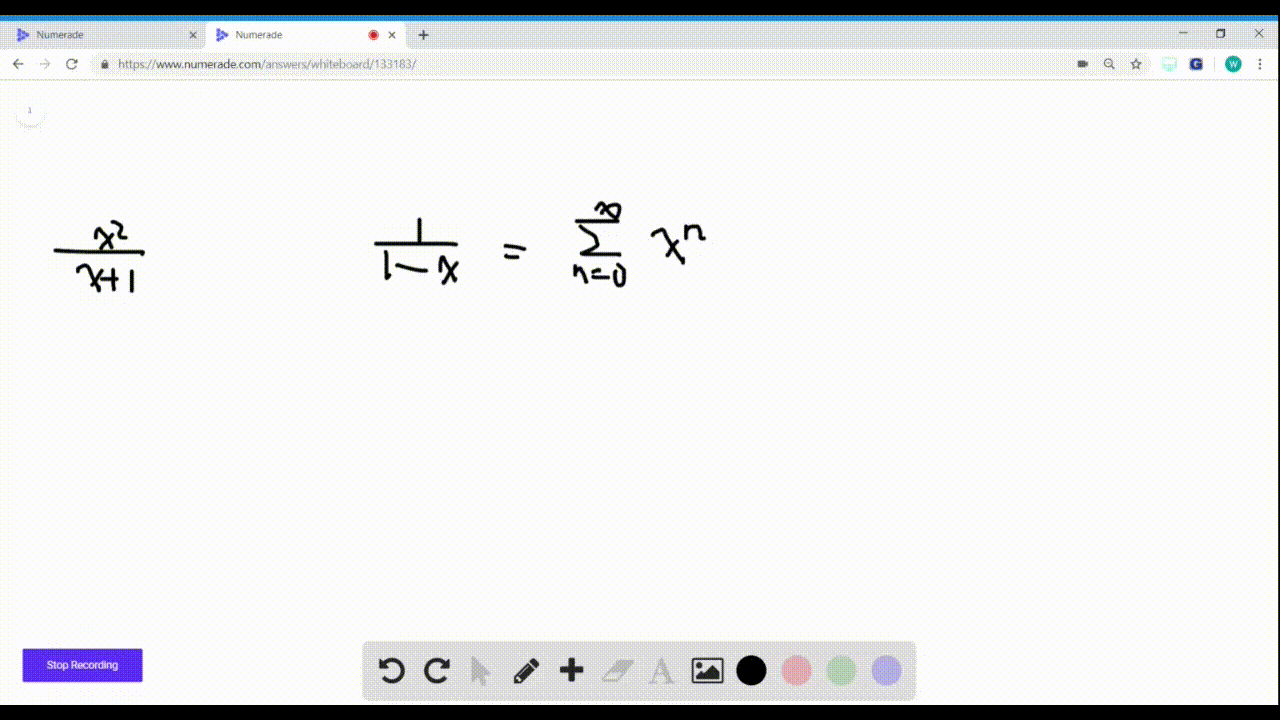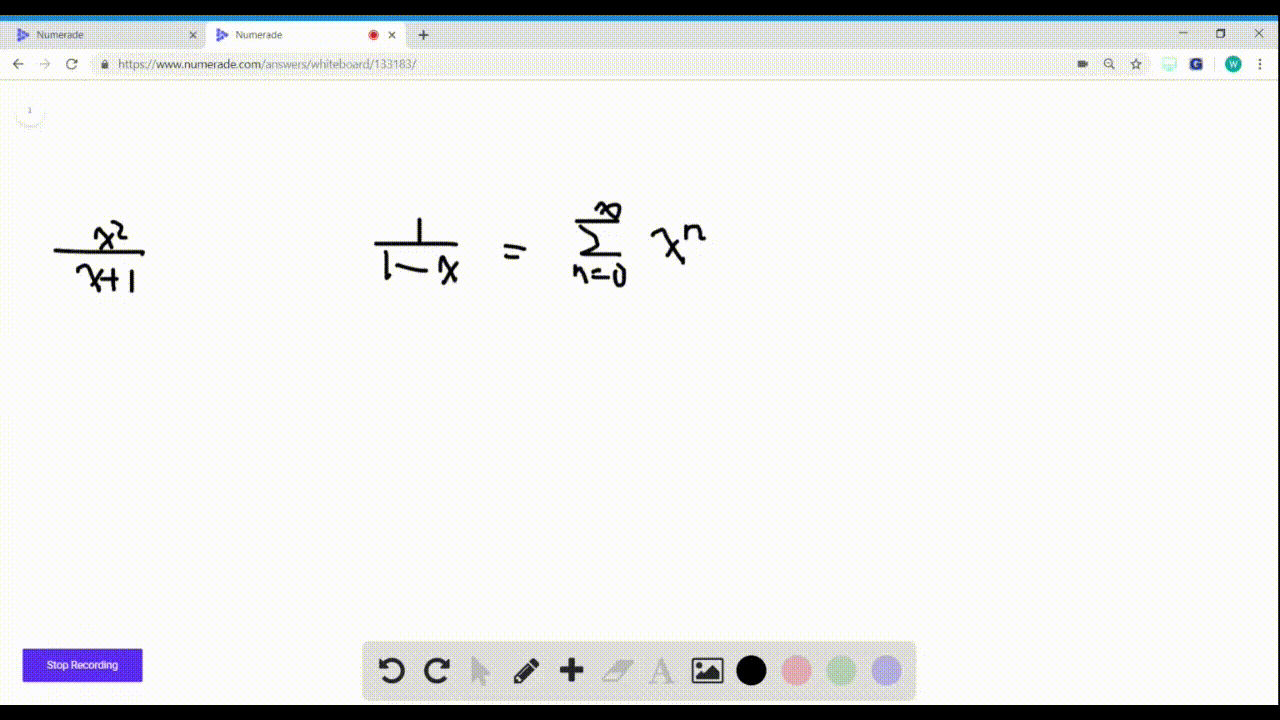
To find a Maclaurin series for ln( 1 +x 1 −x) from scratch, we first need to take note of expressing a function as an infinite sum centered at x = 0. In order to do this, we write. f (x) =. f (0) + f 1(0) 1! x + f 2(0) 2! x2 + f 3(0) 3! x3 +. = ∞ ∑ n=0f n(0) xn n! This infinite sum suggests that we'd have to calculate some derivatives.
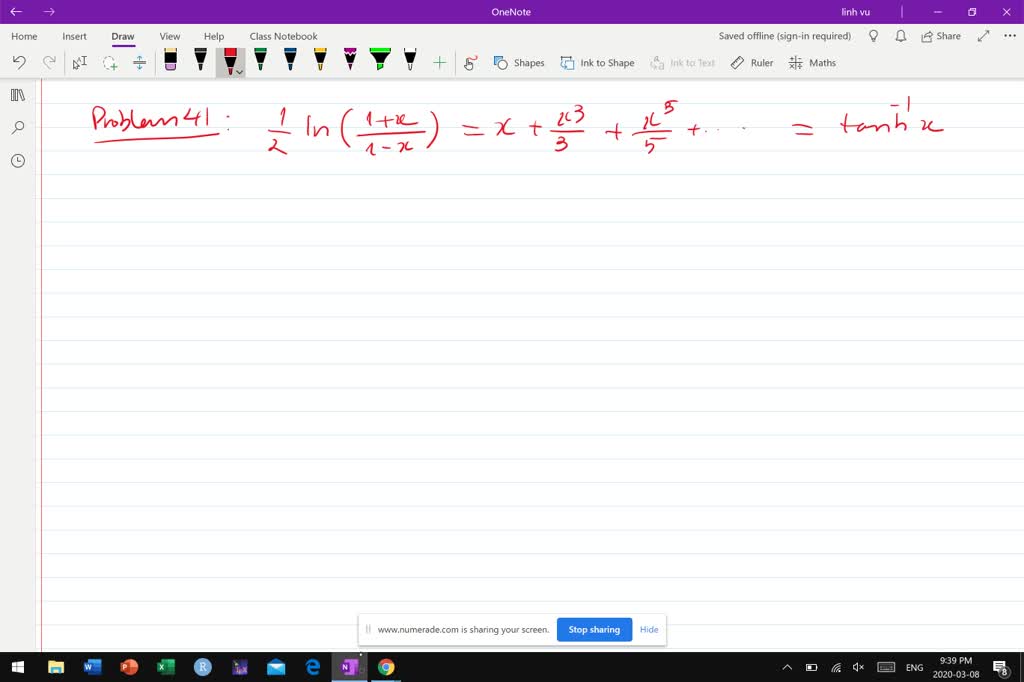
Solved Find the MacLaurin series for ln(1 + x) and ln(1

Deriving the Maclaurin expansion series for ln (1+x) is very easy, as you just need to find the derivatives and plug them into the general formula. As you can see ln1 = 0. Once you differentiate, you end up with a simple reciprocal. Differentiating it again simply increases the power as you can see. In the numerator, you have a factorial.
SOLVEDUse the Maclaurin series for \ln (1+x) and…
A Maclaurin series is a Taylor series expansion of a function about 0, (1) Maclaurin series are named after the Scottish mathematician Colin Maclaurin. The Maclaurin series of a function f(x) up to order n may be found using Series[f, {x, 0, n}]. The nth term of a Maclaurin series of a function f can be computed in the Wolfram Language using SeriesCoefficient[f, {x, 0, n}] and is given by the.
Maclaurin Series

The Maclaurin Series is a special case of the Taylor Series centered at x = 0 x = 0. In a power series, a function is expressed as the sum of terms involving powers of x x, often from x0 x 0 (the constant term) to higher powers. The calculator will find the Taylor (or power) series expansion of the given function around the given point, with.
.

